基于特征脸的人脸识别
原文: http://openbio.sourceforge.net/resources/eigenfaces/eigenfaces.pdf
作者:Dimitri PISSARENKO 时间:2002年12月1日
总目
该记录是基于 M. Turk and A. Pentland(1991b)、 M. Turk and A. Pentland(1991a)和 Smith(2002)文献所作。
特征脸是怎么工作的?
人脸识别的任务本质就是:区别开一些输入信号(图像数据),将其划分进一些分类(人脸)中。
输入信号高度噪声(例如噪声是由不同引起的: 照明条件,姿势等),但输入图像不是完全随机的 尽管它们有差异,但是在任何输入信号中都存在模式。这样 在所有信号中可以观察到的模式可能是在面部识别领域。 任何面孔以及亲属中存在某些物体(眼睛,鼻子,嘴巴) 这些物体之间的距离。这些特征被称为特征脸 面部识别领域(或主要组成部分)。它们可以通过名为PCA(主成分分析法)的数学方法从原始图像数据中提取出来。 通过 PCA 可以能够将训练集的每个原图转化为相关的特征脸。PCA 一个重要的特征是能够组合特征脸来重构训练集中的原图。
记住特征脸不仅仅是面部的特征。所以说如果将每个特征脸按照正确的比例相加,原始脸部图像可以从特征脸重构出来。每个特征脸代表脸部都某些特征,其可能存在或不存在于原图中。如果特征以较高程度表现在原图中,则该特征对应的特征脸应该在特征脸集合相加的总和中,占用更大的比例。相反,特定的特征在原始图像中不存在(或几乎不存在),然后相应的特征脸应该贡献一个较小的(或根本不是)部分的总和。
因此,为了从特征脸重构原始图像,需要得到一系列特征脸的权重,也就是说,重构的原图图像等于所有特征面的总和,每个特征脸都有明确的权重。这个权重表示了指定特征(特征脸)在原图中所占的程度。
如果使用从原始图像提取的所有特征脸,可以重构来自特征脸的原始图像。但也可以只使用一部分特征脸,重建的图像是原始图像的近似值。然而,这样可以确保由于省略某些特征脸而造成的损失最小化,选择最重要的特征(特征脸)。
由于计算资源的匮乏,特征脸的部分选择(降维)是必要的。那这与人脸识别有什么关系呢?不仅可能从给定的一组权重的特征脸得到面部,但也可以用相反的方式,从特征脸和原人脸面部得到一组权重。使用这个权重可以确定两件重要的事情: 1. 确定所讨论的图像是否是一张脸。
输入图像的权重与人脸图像(我们知道是人脸)的权重相差太大,则该输入不是人脸。 2. 相似的脸(图像)具有相似的特征(特征脸)权重。 可以从所有可用的图像中提取权重,通过权重可以进行分组到集群。也就是说,具有相似权重的所有图像可能是类似的面孔。
算法概述
- 首先,将训练集的原始图像转换为一组特征脸 E。
- 然后,计算每个图像在 E 上的一组权重,保存在 W。
观察未知图像 X,计算取特征权重,存储在向量 Wx 中。之后,将Wx与知道他们是面孔(训练的权重W)的其他权重进行比较。一种方法是将每个权重向量视为空间中的一个点计算来自WX的权重向量与权重之间的平均距离D.未知图像的矢量WX(附录A中描述的欧几里德距离)。如果该平均距离超过某个阈值θ,那么未知图像WX的权重向量也与权重“分开”的脸。在这种情况下,未知X被认为不是脸。否则(如果X实际上是一个脸),它的权重向量WX被存储以备以后分类。最优经验性地确定阈值θ。
特征向量和特征值
矩阵的特征向量是一个向量,其与矩阵相乘,则结果总为该向量的整数倍。这个整数值是相应的特征向量的特征值。这种关系可以用公式 M × u = λ × u 来描述,其中u是矩阵M的特征向量,λ是相应的特征值。 特征向量具有以下属性:
- 它们只能用于方阵
- n×n矩阵中有n个特征向量(和相应的特征值)
- 所有特征向量都是垂直的,即彼此成直角
特征脸的计算(PCA 方法)
在本节中,使用PCA确定特征脸的原始方案将会 被呈现。 在本文范围内描述的算法是一个变体。在PCA中可以找到一个详细的(以及更理论的)PCA的描述(Pissarenko,2002,第70-72页)。 1. 准备数据
在这个步骤中,应准备有人脸组成的训练集(Γi)
减去平均值
应当计算出来平均矩阵Ψ,然后从Γi中减去, 并将结果存储在变量Φi中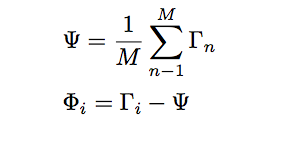
计算协方差矩阵
计算协方差矩阵 C,依据如下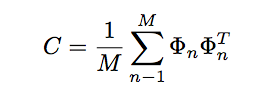
计算协方差的特征向量和特征值矩阵
在这个步骤中,特征向量(特征脸)ui和对应的特征值λi应该计算。特征向量(特征面)必须被归一化才能使它们成为单位向量,即长度为1。描述确定的特征向量和特征值求法在此省略,因为它属于标准的数学程式。选择主要组件
从M个特征向量(特征脸)ui中,只应选择具有最高特征值的M0。特征值越高,特定特征向量描述的面的特征越多。可以省略具有低特征值的特征面,因为它们只解释了面部特征的一小部分。在确定M0特征脸ui之后,算法“训练”阶段结束。
改进原始算法
第5节描述的算法存在问题。协方差矩阵 在步骤3中(参见等式3)具有N 2×N 2的维数,因此将具有N 2 特征面和特征值。 对于256×256图像,这意味着必须计算65,536×65,536个矩阵,并计算65,536个特征面。在计算上,这并不是非常有效,因为大多数这些特征面对我们的任务没有用。所以,第三和第四步被Turk和Pentland(1991a)提出的方案所取代:
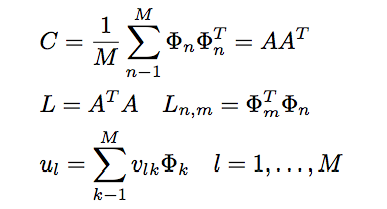
其中L是M×M矩阵,v是L的M个特征向量,u是特征面。 注意 使用公式C = AAT计算协方差矩阵C。只有为了解释A,才给出原始(低效)公式。这种方法的优点是必须只评估M数而不是N2。通常,仅作为主要成分(特征面)的M N2将是相关的。要执行的计算量从训练集(N)的数量减少到训练集(M)中的图像数量。
在步骤5中,相关联的特征值允许根据它们的有用性对特征面进行排序。 通常,我们将仅使用M个特征面的一个子集,具有最大特征值的M0特征面。
人脸分类
新的人脸(未知)分类至已知人脸中需要2个步骤。
首先,得到新人脸的特征脸,得到权重向量 ΩT(new)
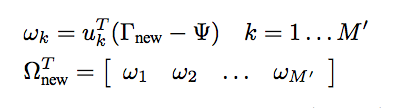
两个权重向量的欧几里得距离 d(Ωi, Ωj) 提供了一种衡量图像 i、j 的相似度的方法。如果ΩT(new)与其他人脸平均超过阈值θ,则认为其非人脸,或者构造一个新的脸的“簇”,使得类似的面部被分配给一个群集。
欧几里得距离
x 为被特征向量描述的任意实例。
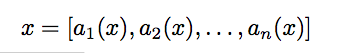
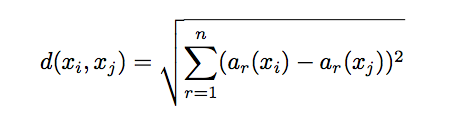
参考文献
- T. M. Mitchell. Machine Learning. McGraw-Hill International Editions, 1997.
- D. Pissarenko. Neural networks for financial time series prediction: Overview over recent research. BSc thesis, 2002.
- L. I. Smith. A tutorial on principal components analysis, February 2002. URL http://www.cs.otago.ac.nz/cosc453/student_tutorials/principal_components.pdf. (URL accessed on November 27, 2002).
- M. Turk and A. Pentland. Eigenfaces for recognition. Journal of Cognitive Neuroscience, 3(1), 1991a. URL http://www.cs.ucsb.edu/~mturk/Papers/jcn. pdf. (URL accessed on November 27, 2002).
- M. A. Turk and A. P. Pentland. Face recognition using eigenfaces. In Proc. of Computer Vision and Pattern Recognition, pages 586–591. IEEE, June 1991b. URL http: //www.cs.wisc.edu/~dyer/cs540/handouts/mturk-CVPR91.pdf. (URL accessed on November 27, 2002).