(译) O(ND)字符串差异算法

由于以前的markdown编辑器涉及到diff算法，接触到了diff-match-patch.js
相关的论文与代码均在 https://code.google.com/p/google-diff-match-patch/

An O(ND) Difference Algorithm and Its Variations∗

EUGENE W. MYERS
Department of Computer Science, University of Arizona, Tucson, AZ 85721, U.S.A.

作者： 亚利桑那大学计算机科学系，EUGENE W.MYERS

The problems of finding a longest common subsequence of two sequences A and B and a shortest edit script for transforming A into B have long been known to be dual problems. In this paper, they are shown to be equivalent to finding a shortest/longest path in an edit graph. Using this perspective, a simple O(ND) time and space algorithm is developed where N is the sum of the lengths of A and B and D is the size of the minimum edit script for A and B. The algorithm performs well when differences are small (sequences are similar) and is consequently fast in typical applications. The algorithm is shown to have O(N + D 2 ) expected-time performance under a basic stochastic model. A refinement of the algorithm requires only O(N) space, and the use of suffix trees leads to an O(NlgN + D 2 ) time variation.

众所周知，寻找最长公共子串问题(LCS)与最短编辑脚本问题(SES)是对偶问题。在这篇论文中，他们将被认为在编辑图中寻找最短/最长路径是等价问题。在这个视角看该问题，O(ND)时间空间复杂度的算法就出现了，N表示A串、B串的长度之和，D表示A、B的最小编辑脚本。该算法在A、B串差异不大的时候效率很好(D很小)。该算法在一般随机的情况下，有O(N+D²)的预计时间效率和O(N)的空间复杂度，如果使用前缀树的话，时间复杂度可以优化至O(NlgN+D²).

KEY WORDS
longest common subsequence shortest edit script edit graph file comparison

关键词：
最长公共子串；最短编辑脚本(LCS)；编辑图(SES)；文件比对

Introduction

引言

The problem of determining the differences between two sequences of symbols has been studied extensively [1,8,11,13,16,19,20]. Algorithms for the problem have numerous applications, including spelling correction systems, file comparison tools, and the study of genetic evolution [4,5,17,18]. Formally, the problem statement is to find a longest common subsequence or, equivalently, to find the minimum ‘‘script’’ of symbol deletions and insertions that transform one sequence into the other. One of the earliest algorithms is by Wagner & Fischer [20] and takes O(N 2 ) time and space to solve a generalization they call the string-to-string correction problem. A later refinement by Hirschberg [7] delivers a longest common subsequence using only linear space. When algorithms are over arbitrary alphabets, use ‘‘equal—unequal’’ comparisons, and are characterized in terms of the size of their input, it has been shown that Ω(N 2 ) time is necessary [1]. A ‘‘Four Russians’’ approach leads to slightly better O(N 2 lglgN/lgN) and O(N 2 /lgN) time algorithms for arbitrary and finite alphabets respectively [13]. The existence of faster algorithms using other comparison formats is still open. Indeed, for algorithms that use ‘‘less than—equal—greater than’’ comparisons, Ω(NlgN) time is the best lower bound known [9].

两个字符串差异问题已经在其他的文献中有过学习[1,8,11,13,16,19,20]。应用该算法的应用有许多，包括拼写校对系统，文件比对工具，基因演化的研究[4,5,17,18]。进入正题，寻找最长公共子串的问题等价于最短编辑脚本(A串通过若干插入和删除操作变为B串的操作数)。其中最早的算法是来自Wagner和Fischer的"串串"校对问题，需要O(N²)的时空复杂度。之后是来自Hirschberg的优化，只需要O(N)线性空间复杂度[7]。当差异算法是基于相等不相等的比较操作，则被认为Ω(N²)是必须的[1]。随后有四位俄罗斯人做出了略微地优化，将时间复杂度降至O(N²lglgN/lgN)和O(N²/lgN)，分别对应随机字母情况和有限字母情况。当然还存在更快的基于其他比较操作算法，事实上，使用"<=" "=" ">="比较操作的算法，Ω(NlgN)时间复杂度是最佳的。

Recent work improves upon the basic O(N 2 ) time arbitrary alphabet algorithm by being sensitive to other problem size parameters. Let the output parameter L be the length of a longest common subsequence and let the dual parameter D = 2(N − L) be the length of a shortest edit script. (It is assumed throughout this introduction that both strings have the same length N.) The two best output-sensitive algorithms are by Hirschberg [8] and take O(NL + NlgN) and O(DLlgN) time. An algorithm by Hunt & Szymanski [11] takes O((R+ N) lgN) time where the parameter R is the total number of ordered pairs of positions at which the two input strings match. Note that all these algorithms are Ω(N 2 ) or worse in terms of N alone.

最近有研究提升了随机字母情况的O(N²)算法，使得该问题效率对另一个参数敏感。假设输出参数L为最长公共子序列长度，那么对应的对偶参数D = 2*(N-L)，表示最短编辑脚本长度。(在引言中，假定A、B串长都为N) 有两个来自Hirschberg输出敏感算法，分别需要O(NL+NlgN) 和 O(DLlgN) 时间复杂度。还有一种来自Hunt和Szymanski的O((R+N)lgN)算法，R表示AB串相等的位置个数。

In practical situations, it is usually the parameter D that is small. Programmers wish to know how they have altered a text file. Biologists wish to know how one DNA strand has mutated into another. For these situations, an O(ND) time algorithm is superior to Hirschberg’s algorithms because L is O(N) when D is small. Furthermore, the approach of Hunt and Szymanski [11] is predicated on the hypothesis that R is small in practice. While this is frequently true, it must be noted that R has no correlation with either the size of the input or the size of the output and can be O(N 2 ) in many situations. For example, if 10% of all lines in a file are blank and the file is compared against itself, R is greater than .01N 2 . For DNA molecules, the alphabet size is four implying that R is at least .25N 2 when an arbitrary molecule is compared against itself or a very similar molecule.

在实际情况下，通常参数D比较小。比如程序员想要知道他们曾经对于文本文件的修改。生物学家想知道DNA的突变情况。对于这些情况，O(ND)算法更优于Hirschberg的算法，因为当D比较小的时候，L需要O(N)时间才能求出。

In this paper an O(ND) time algorithm is presented. Our algorithm is simple and based on an intuitive edit graph formalism. Unlike others it employs the ‘‘greedy’’ design paradigm and exposes the relationship of the longest common subsequence problem to the single-source shortest path problem. Another O(ND) algorithm has been presented elsewhere [16]. However, it uses a different design paradigm and does not share the following features. The algorithm can be refined to use only linear space, and its expected-case time behavior is shown to be O(N + D 2 ). Moreover, the method admits an O(NlgN + D 2 ) time worst-case variation. This is asymptotically superior to previous algorithms [8,16,20] when D is o(N).

在这篇论文中将给出一个O(ND)时间复杂度的算法。我们的算法简单，并且基于便于理解的编辑图。它利用“贪心”的设计范例，表现了最长公共子序列到单源最短路径的关系。一个其他的O(ND)算法在其他地方被提出来[16]。然而，它使用的是不同的贪心策略，而且也没有提出什么相关的特性。该算法可以优化至线性空间复杂度。

Edit Graphs

编辑图

Let A = a 1 a 2 . . . a N and B = b1 b2 . . . b M be sequences of length N and M respectively. The edit graph for A and B has a vertex at each point in the grid (x,y), x∈[0,N] and y∈[0,M]. The vertices of the edit graph are connected by horizontal, vertical, and diagonal directed edges to form a directed acyclic graph. Horizontal edges connect each vertex to its right neighbor, i.e. (x−1,y)→(x,y) for x∈[1,N] and y∈[0,M]. Vertical edges connect each vertex to the neighbor below it, i.e. (x,y−1)→(x,y) for x∈[0,N] and y∈[1,M]. If a x = by then there is a diagonal edge connecting vertex (x−1,y−1) to vertex (x,y). The points (x,y) for which a x = by are called match points. The total number of match points between A and B is the parameter R characterizing the Hunt & Szymanski algorithm [11]. It is also the number of diagonal edges in the edit graph as diagonal edges are in one-to-one correspondence with match points. Figure 1 depicts the edit graph for the sequences A = abcabba and B = cbabac.

设A=a1a2a3...aN, B=b1b2b3...bM, len(A)=N,len(B)=M，则AB的编辑图就是x∈[0,N], y∈[0,M]，组成的一个二维网格图。编辑图的顶点可以通过有向无环图的水平，垂直，斜线边连接。水平边如(x-1,y)->(x,y), x∈[1,N], y∈[0,M]. 垂直边如(x,y-1)->(x,y), x∈[0,N] y∈[1,M]. 如果ax=by，则存在斜边(x-1,y-1)->(x,y), 像这样的点(x,y)被叫做“配对点”。配对点的总数就是Hunt&Szymanski算法中的相关参数R，也就是编辑图中的斜边个数。图1描绘了串A"abcabba"和串B"cbabac"的编辑图。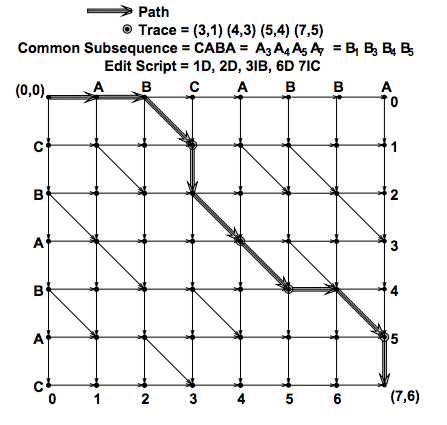

A trace of length L is a sequence of L match points, (x1 ,y1 )(x2 ,y2 ) . . . (x L ,y L ), such that xi < xi + 1 and yi < yi + 1 for successive points (xi ,yi ) and (xi + 1 ,yi + 1 ), i∈[1,L−1]. Every trace is in exact correspondence with the diagonal edges of a path in the edit graph from (0,0) to (N,M). The sequence of match points visited in traversing a path from start to finish is easily verified to be a trace. Note that L is the number of diagonal edges in the corresponding path. To construct a path from a trace, take the sequence of diagonal edges corresponding to the match points of the trace and connect successive diagonals with a series of horizontal and vertical edges. This can always be done as xi < xi + 1 and yi < yi + 1 for successive match points. Note that several paths differing only in their non-diagonal edges can correspond to a given trace. Figure 1 illustrates this relation between paths and traces.

L的痕迹(trace)是L个配对点的序列，也就是xi<x(i+1)并且yi<y(i+1)。每一个痕迹都准确地配对从(0,0)到(N,M)的斜边。在从起点到终点遍历的过程中，trace就被标记出来了。注释：L就是从起点到终点的斜边个数。如图，(0,0)到(N,M)的路径有很多，但痕迹是路径的子集。

An edit script for A and B is a set of insertion and deletion commands that transform A into B. The delete command ‘‘xD’’ deletes the symbol a x from A. The insert command ‘‘x I b1 ,b2 , . . . bt ’’ inserts the sequence of symbols b1 . . . bt immediately after a x . Script commands refer to symbol positions within A before any commands have been performed. One must think of the set of commands in a script as being executed simultaneously. The length of a script is the number of symbols inserted and deleted

A和B的编辑脚本是将A转换为B的插入和删除操作的集合。"xD"表示删除ax，"xIb1,b2,...bt"表示在ax之后插入b1,b2,...,bt。这些操作是同时进行的。脚本的长度就是插入和删除字符的个数。

The problem of finding a longest common subsequence (LCS) is equivalent to finding a path from (0,0) to (N,M) with the maximum number of diagonal edges. The problem of finding a shortest edit script (SES) is equivalent to finding a path from (0,0) to (N,M) with the minimum number of non-diagonal edges. These are dual problems as a path with the maximum number of diagonal edges has the minimal number of non-diagonal edges (D+2L = M+N). Consider adding a weight or cost to every edge. Give diagonal edges weight 0 and non-diagonal edges weight 1. The LCS/SES problem is equivalent to finding a minimum-cost path from (0,0) to (N,M) in the weighted edit graph and is thus a special instance of the single-source shortest path problem.

显而易见，将A转变为B，需要删除N-L个字符，插入M-L个字符，所以编辑脚本的长度D=N+M-2L。 所以公共子串问题，编辑脚本问题，痕迹问题，(0,0)到(N,M)路径问题都是同一类问题。路径上的水平和垂直线就是对应删除插入操作。最长公共子序列问题就是寻找(0,0)到(N,M)具有最多斜边数目的路径；最小编辑脚本问题就是寻找(0,0)到(N,M)具有最少非斜边数目的路径，显然这是一对对偶问题。

An O((M+N)D) Greedy Algorithm

O((M+N)*D)的贪心算法

The problem of finding a shortest edit script reduces to finding a path from (0,0) to (N,M) with the fewest number of horizontal and vertical edges. Let a D-path be a path starting at (0,0) that has exactly D non-diagonal edges. A 0-path must consist solely of diagonal edges. By a simple induction, it follows that a D-path must consist of a (D − 1)-path followed by a non-diagonal edge and then a possibly empty sequence of diagonal edges called a snake.

找到最短编辑脚本的问题可以简化为找一条从(0,0)到(N,M)的path，同时满足水平边和垂直边最少。假定D-path表示从(0,0)出发，有D条非对角边。那么0path必须由纯粹的对角边组成。通过一个简单的归纳，D-path也必须由一个(D-1)-path跟随在一个对角边后组成，于是将剩下的对角边（可能是空的）称为snake。

Number the diagonals in the grid of edit graph vertices so that diagonal k consists of the points (x,y) for which x − y = k. With this definition the diagonals are numbered from −M to N. Note that a vertical (horizontal) edge with start point on diagonal k has end point on diagonal k − 1 (k + 1) and a snake remains on the diagonal in which it starts.

将编辑图中对角边进行编码，对角边K就有一系列点(x,y)组成，x-y=k. 通过这样的定义，编码就是从-M到N。注意垂直（水平）边在对角边K上都有开始点，在对角边k-1(k+1)上都有个结束点，snake就在对角边的开始处。

Lemma 1:
A D-path must end on diagonal k ∈ { − D, − D + 2, . . . D − 2, D }.

Proof:
A 0-path consists solely of diagonal edges and starts on diagonal 0. Hence it must end on diagonal 0. Assume inductively that a D-path must end on diagonal k in { − D, − D + 2, . . . D − 2, D }. Every (D+1)-path consists of a prefix D-path, ending on say diagonal k, a non-diagonal edge ending on diagonal k+1 or k−1, and a snake that must also end on diagonal k+1 or k−1. It then follows that every (D+1)-path must end on a diagonal in { (−D)±1, (−D+2)±1, . . . (D−2)±1, (D)±1 } = { −D−1, −D+1, . . . D−1, D+1 }. Thus the result holds by induction. ✂ The lemma implies that D-paths end solely on odd diagonals when D is odd and even diagonals when D is even.

A D-path is furthest reaching in diagonal k if and only if it is one of the D-paths ending on diagonal k whose end point has the greatest possible row (column) number of all such paths. Informally, of all D-paths ending in diagonal k, it ends furthest from the origin, (0,0). The following lemma gives an inductive characterization of furthest reaching D-paths and embodies a greedy principle: furthest reaching D-paths are obtained by greedily extending furthest reaching (D − 1)-paths

理论 1：一条D-path必须终止在一条对角边上k, k属于(-D,-D+2,….D-2,D)

证明： 一条0-path由许多纯粹的对角边组成并且开始于对角边0。因此，他必须终止在对角边0上。假设一条D-path在对角边k上终止，k属于{-D,-D+2,…D-2,D}。那么每一个(D+1)-Path也由前一个终止在对角边k上的D-Path，和终止在对角边k+1或者k-1的非对角边组成，snake也同样终止在k+1或者k-1。于是，每一个(D+1)-path必须终止在对角边{ (-D)±1, (-D+2)±1, . . . (D-2)±1, (D)±1 } = { -D-1, -D+1, . . . D-1, D+1 }。

Lemma 2:
A furthest reaching 0-path ends at (x,x), where x is min( z−1 || a z ≠bz or z>M or z>N). A furthest reaching D-path on diagonal k can without loss of generality be decomposed into a furthest reaching (D − 1)-path on diagonal k − 1, followed by a horizontal edge, followed by the longest possible snake or it may be decomposed into a furthest reaching (D − 1)-path on diagonal k+1, followed by a vertical edge, followed by the longest possible snake.

理论2：
一条最远的0-path必然结束在(x,x)上，x为最小的( z-1 | a z 不等于bz 或者z>M 或者 z>N).一条最远的对角边k上的D-path， 可以分解为一条最远的对角边k+1上的(D-1)-path，该对角边跟随在一条水平边之后，跟随在最长的snake后面；或者该对角边跟随在一条垂直边之后，跟随在最长的snake后面。

Proof:
The basis for 0-paths is straightforward. As noted before, a D-path consists of a (D − 1)-path, a non-diagonal edge, and a snake. If the D-path ends on diagonal k, it follows that the (D − 1)-path must end on diagonal k±1 depending on whether a vertical or horizontal edge precedes the final snake. The final snake must be maximal, as the D-path would not be furthest reaching if the snake could be extended. Suppose that the (D − 1)-path is not furthest reaching in its diagonal. But then a further reaching (D − 1)-path can be connected to the final snake of the D-path with an appropriate non-diagonal move. Thus the D-path can always be decomposed as desired.
Given the endpoints of the furthest reaching (D − 1)-paths in diagonal k+1 and k−1, say (x’,y’) and (x",y") respectively, Lemma 2 gives a procedure for computing the endpoint of the furthest reaching D-path in diagonal k. Namely, take the further reaching of (x’,y’+1) and (x"+1,y") in diagonal k and then follow diagonal edges until it is no longer possible to do so or until the boundary of the edit graph is reached. Furthermore, by Lemma 1 there are only D+1 diagonals in which a D-path can end. This suggests computing the endpoints of D-paths in the relevant D+1 diagonals for successively increasing values of D until the furthest reaching path in diagonal N − M reaches (N,M)

证明：0-paths的基本是笔直向前的。之前提到过，D-path由一系列(D-1)-path,一个非对角边组成和一条snake组成。如果D-path结束在对角边k上，它必须满足(D-1)-path必须结束在对角边k±1上，并且取决于最终构建snake的是水平边还是垂直边。最终的snake也必须是最长的，也就是当snake延伸的时候，D-path的长度也在增加。假定(D-1)-path在它的对角边上并没有达到最深。但是，之后(D-1)-path可以连接到最终的D-path的snake,通过适当的非对角边变化。此外，D-path可以任意的重组。
给定的最远到达(D-1)-paths在k+1和k-1上的结束点，(x’,y’)和(x",y")，理论2给了一个在对角边k上达到最远D-path的计算过程。即在对角边k上，取更深远的点(x’,y’+1) 和 (x"+1,y")然后沿着对角边，直到它不能再做同样的步骤，或者到达了编辑图的边界。此外，通过理论1，只有D-path才能到达D+1的对角边。这就意味着在相关的D+1对角边上计算D-paths的结束点，不断地增加D值直到最远的对角边N-M到达顶点(N,M)。

The outline above stops when the smallest D is encountered for which there is a furthest reaching D-path to (N,M). This must happen before the outer loop terminates because D must be less than or equal to M+N. By construction this path must be minimal with respect to the number of non-diagonal edges within it. Hence it is a solution to the LCS/SES problem.

上述公式，for语句将会在找到最远的到达(N,M)顶点的D-path的时候停止，即D最小。当然，D也一定比M+N小。通过构建这条路径，我们需要求的非对角边是最小。通过这样的方式，我们就能解决LCS/SES问题。

In presenting the detailed algorithm in Figure 2 below, a number of simple optimizations are employed. An array, V, contains the endpoints of the furthest reaching D-paths in elements V[− D], V[− D + 2], . . . , V[D-2], V[D]. By Lemma 1 this set of elements is disjoint from those where the endpoints of the (D+1)-paths will be stored in the next iteration of the outer loop. Thus the array V can simultaneously hold the endpoints of the D-paths while the (D+1)-path endpoints are being computed from them. Furthermore, to record an endpoint (x,y) in diagonal k it suffices to retain just x because y is known to be x − k. Consequently, V is an array of integers where V[k] contains the row index of the endpoint of a furthest reaching path in diagonal k.

图2描绘了具体的算法过程，也运用了一些简单的优化。使用一个数组V，记录D-paths的结束点V[- D], V[-D+ 2], . . . , V[D-2], V[D]。通过理论1，这组顶点与存储在外界循环的(D+1)-paths的结束点相交。因此，数组V可以持续不断的保存D-paths的结束点，而(D+1)-paths的结束点也是通过它们进行计算的。此外，为了记录(x,y)在对角边k的情况，只需要保留x，因为y可以通过x-k得到。因此，V是一个整数数组，其中V[k]保存了对角边k能到达的最远的结束点的航坐标。

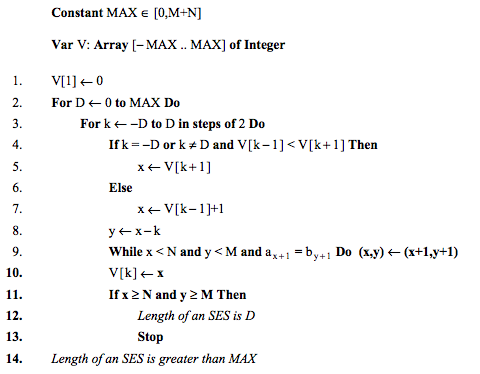
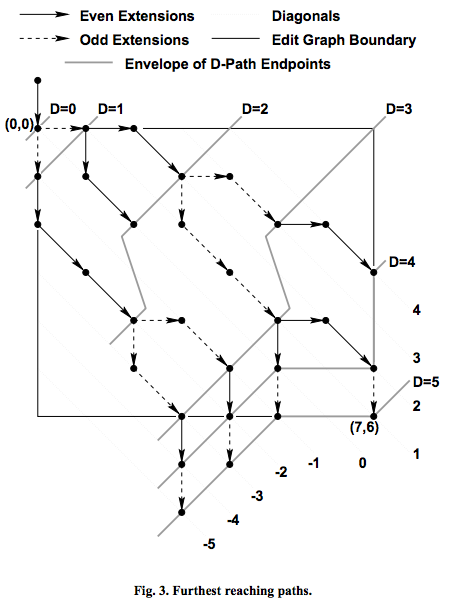
As a practical matter the algorithm searches D-paths where D≤MAX and if no such path reaches (N,M) then it reports that any edit script for A and B must be longer than MAX in Line 14. By setting the constant MAX to M+N as in the outline above, the algorithm is guaranteed to find the length of the LCS/SES. Figure 3 illustrates the Dpaths searched when the algorithm is applied to the example of Figure 1. Note that a fictitious endpoint, (0, − 1), set up in Line 1 of the algorithm is used to find the endpoint of the furthest reaching 0-path. Also note that D-paths extend off the left and lower boundaries of the edit graph proper as the algorithm progresses. This boundary situation is correctly handled by assuming that there are no diagonal edges in this region

事实上，算法到达D-paths时D<=MAX，如果不存在这样的路径能过到达(N,M)，那么关于A和B任何一个脚本的长度都会超过MAX值，如第14行所示。通过设置MAX的值为M+N，算法就能正常的找到LCS/SES的长度。图3显示了D-paths搜索方法，通过对图1的算法应用。注意虚构的点(0,-1)，在公式第一行，该点是用来找到0-path的结束点。同样注意D-paths在编辑图里超过了左边界和下边界，作为算法运算的一部分。这种边界的情况是为了处理假定不存在对角边。

The greedy algorithm takes at most O((M+N)D) time. Lines 1 and 14 consume O(1) time. The inner For loop (Line 3) is repeated at most (D+1)(D+2)/2 times because the outer For loop (Line 3) is repeated D+1 times and during its k th iteration the inner loop is repeated at most k times. All the lines within this inner loop take constant time except for the While loop (Line 9). Thus O(D2 ) time is spent executing Lines 2-8 and 10-13. The While loop is iterated once for each diagonal traversed in the extension of furthest reaching paths. But at most O((M+N)D) diagonals are traversed since all D-paths lie between diagonals − D and D and there are at most (2D+1)min(N,M) points within this band. Thus the algorithm requires a total of O((M+N)D) time. Note that just Line 9, the traversal of snakes, is the limiting step. The rest of the algorithm is O(D2 ). Furthermore the algorithm never takes more than O((M+N)MAX) time in the practical case where the threshold MAX is set to a value much less than M+N.

贪心算法最多消耗O((M+N)D)时间。第一行和第十四行只用了O(1)的时间，内嵌的For语句循环(第三行)最多重复(D+1)(D+2)/2次，因为外部循环For语句(第三行)重复了D+1次，然后由于k指针最多运行k次。所有的操作都是常数时间，除了内嵌的While语句（第9行）。因此，第2到第8行，第10到第13行，一共用了O(DD)的时间。While语句也只执行一次，如果能通过对角边直接达到最大值。但是大多数时候，需要花费O((M+N)D)的时间，因为所有-D到D之间的D-pahts需要花费(2D+1)乘以最小的(N,M)。所以，算法一共需要O((M+N)D)的时间。注意第9行，构造Snake，用来判断是否跳出循环。其余的算法需要O(D*D)的时间。此外，在实际情况下，如果MAX的值小于M+N,该算法的效率不会超过O((M+N)MAX)。 这里，第一层循环最大可以理解为D+1(最坏情况下是M+N)次，第二层循环k是跟着D在改变的，最坏情况也是(M+N)。所以时间是线性递增，最坏情况就是O((M+N)D)

The search of the greedy algorithm traces the optimal D-paths among others. But only the current set of furthest reaching endpoints are retained in V. Consequently, only the length of an SES/LCS can be reported in Line 12. To explicitly generate a solution path, O(D 2 ) space ∗ is used to store a copy of V after each iteration of the outer loop. Let Vd be the copy of V kept after the d th iteration. To list an optimal path from (0,0) to the point Vd [k] first determine whether it is at the end of a maximal snake following a vertical edge from Vd − 1 [k + 1] or a horizontal edge from Vd − 1 [k − 1]. To be concrete, suppose it is Vd − 1 [k − 1]. Recursively list an optimal path from (0,0) to this point and then list the vertical edge and maximal snake to Vd [k]. The recursion stops when d = 0 in which case the snake from (0,0) to (V0 [0],V0 [0]) is listed. So with O(M+N) additional time and O(D 2 ) space an optimal path can be listed by replacing Line 12 with a call to this recursive procedure with VD [N − M] as the initial point. A refinement requiring only O(M+N) space is shown in the next section.

因为贪心算法追踪了一条可行的D-paths。但是，它仅仅是把最深的对角结束点保存在数组V中。因此，第十二行也只是单单的列出了最小SES/LCS长度。为了明确的生成这样的一条路径，我们仍然需要O(D*D)的空间保持V，当V结束了外部循环后。让Vd保存d遍历后的V值。为了列出从(0,0)点到Vd[k]，首先，我们需要确定它是否是最大Snake的终点，并且之前的水平边来自Vd-1[k+1]，或者垂直边来自Vd-1[k-1]。具体来说，假定是Vd-1[k-1]。然后递归列出一条从(0,0)到达该点的路径，然后列出垂直边以及最大Snake到达Vd[k]。递归需要在d=0的时候结束，Snake从(0,0)到达(V0[0],V0[0])。因此，我们还需要在第十二行增加额外的O(M+N)的时间和O(D*D)的空间，对于这个递归，我们需要起点为Vd[N-M]。 下一部分，该算法的空间可以降低为O(M*N)

As noted in Section 2, the LCS/SES problem can be viewed as an instance of the single-source shortest paths problem on a weighted edit graph. This suggests that an efficient algorithm can be obtained by specializing Dijkstra’s algorithm [3]. A basic exercise [2: 207-208] shows that the algorithm takes O(ElgV) time where E is the number of edges and V is the number of vertices in the subject graph. For an edit graph E < 3V since each point has outdegree at most three. Moreover, the lgV term comes from the cost of managing a priority queue. In the case at hand the priorities will be integers in [0,M+N] as edge costs are 0 or 1 and the longest possible path to any point is M+N. Under these conditions, the priority queue operations can be implemented in constant time using ‘‘bucketing’’ and linked-list techniques. Thus Dijkstra’s algorithm can be specialized to perform in time linear in the number of vertices in the edit graph, i.e. O(MN). The final refinement stems from noting that all that is needed is the shortest path from the source (0,0) to the point (M,N). Dijkstra’s algorithm determines the minimum distances of vertices from the source in increasing order, one vertex per iteration. By Lemma 1 there are at most O((M+N)D) points less distant from (0,0) than (M,N) and the previous refinements reduce the cost of each iteration to O(1). Thus the algorithm can stop as soon as the minimum distance to (M,N) is ascertained and it only spends O((M+N)D) time in so doing.

正如第二部分所说的，LCS/SES可以看做是在有权编辑图中的单源最短路问题。这就是说我们可以利用特定的Dijkstra’s[3]的算法得到更高效的算法。一个基本的联系[2: 207-208]显示了算法只需要O(ElgV)的时间，E为变得数量，V为主题图中点的匹配点的数量。对于编辑图E<3V，因为每个点的出度都有3个。此外，lgV可以从保持较好的队列获得。实际上，我们可以手动开辟一个整数队列[0,M+N]，因为边的花费不是0就是1，能够遍历任何节点的长度也不超过M+N。在这样的条件下，优先队列可以应用成装箱问题以及链表问题。因此Dijkstra’s的算法可以线性的优化算法，到点的数量，比如O(M*N)。最终的优化所有从(0,0)到(M,N)的最短路问题。Dijkstra’s的算法决定了最小的距离。通过理论1，从(0,0)出发，比起(M,N)，最多有O((M+N)D得点有更少的距离，而且先前的优化也能将遍历缩减为O(1)。因此，该算法在遇到最短距离是，就会停止。